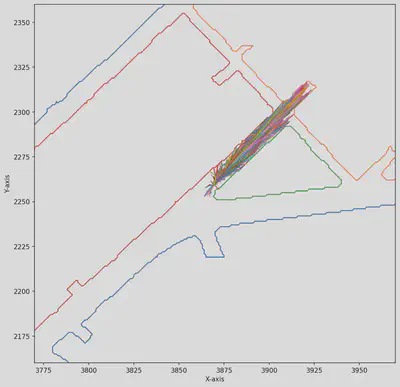
Point-in-Polygon Checking for trajectories: Without Parallelization

This is a two-part version of how the Point-in-Polygon(PIP) algorithm is implemented in my paper Knowledge Integrated Plausible Motion Forecasting. I had to skip this part in the paper because it deserved its appreciation post.
Part-1 Normal version without any parallelization
Given a scene representation, it is essential to eliminate trajectories that venture into non-drivable areas. This pruning process is crucial due to the inherent epistemic uncertainty present in neural networks, which can lead to the prediction of infeasible situations. This uncertainty primarily arises from a lack of domain knowledge.
The scene representation consists of polygon’s area representing the non-drivable zones, with the number of polygons varying depending on the complexity of the scene. It is assumed that at least one polygon is present per scene. Prior to the pruning process, the set of trajectories remains constant across all scenes, with a shape of (2206, 30, 2). Here, 2206 represents the total number of trajectories, while (30, 2) indicates that each trajectory is composed of 30 coordinate points, with each point represented by its x and y values. By removing the trajectories that intersect with non-drivable areas, the system can ensure that the remaining trajectories are physically feasible and adhere to the constraints of the environment.
1. Loading the HD maps and Trajectory sets
You can load the files from [here](Place the github link). I reduced the whole raw data to just the HD maps; and the trajectories are rotated to fit the direction vector calculated through the heading angle of the target actor (the object for which we’re doing a forecasting for)
def load_pickle(file_name):
with open(file_name, 'rb') as f:
return pickle.load(f)
def just_load_das_traj(file_number=1):
local_das = load_pickle(f'local_das/local_das{file_number}.pkl')
# print(f"local das dtype: {local_das.shape}")
rotated_traj = load_pickle(f'rotated_traj/rotated_traj{file_number}.pkl')
#Control how many trajectories you want to load here
trajectories = rotated_traj
return local_das, trajectories
2. Helper function for visualization
The function takes in drivable areas and rotated trajectories to plot it onto a Matplotlib axes canvas.
def plot_things(local_drivable_areas, trajectory, ax=None)->None:
"""
local_drivable_areas: np.array
trajectory: np.array
"""
center = (trajectory[0,0,0], trajectory[0,0,1])
offset = 100
xx,xy = center[0]-offset, center[0]+offset
yy,yx = center[1]-offset, center[1]+offset
# Add labels and title
ax.set_xlim(xx, xy)
ax.set_ylim(yy, yx)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
for i in local_drivable_areas:
ax.plot(*Polygon(i).exterior.xy)
for i in trajectory:
ax.plot(i[:,0], i[:,1])
3. Helper functions to aid the pruning
def create_buffer_around_coordinate(coordinate, radius):
point = Point(coordinate)
buffer_polygon = point.buffer(radius)
return buffer_polygon
def check_intersection(trajectory, polygons):
if any(trajectory.intersects(polygons)):
return False
return True
def check_linestring_intersects(trajectory, target_linestring):
if trajectory.intersects(target_linestring):
return False
return True
def calculate_intersection_polygons(original_poly, buffer_polygon):
intersecting_polygons = []
# Iterate over each polygon in the original multipolygon
for idx, polygon_k in enumerate(original_poly):
# Get the intersection between the current polygon and the buffer polygon
intersection_polygon = polygon_k.intersection(buffer_polygon)
# Check if the intersection is not empty and is a polygon or multipolygon
if intersection_polygon.geom_type in ['Polygon']:
intersecting_polygons.append(intersection_polygon)
elif intersection_polygon.geom_type in ['MultiPolygon']:
individual_polygons = list(intersection_polygon.geoms)
for polygons in individual_polygons:
intersecting_polygons.append(polygons)
return intersecting_polygons
def calculate_intersection_polygons_main_map(give_me_ring, buffer_polygon_main_map):
intersection_boundary_linearring = []
# We need to construct a local buffer and collect the intersection polygons
for linearring in give_me_ring:
# Get the intersection between the current polygon and the buffer polygon
local_intersection_poly = linearring.intersection(buffer_polygon_main_map)
# Check if the intersection is not empty and is a polygon or multipolygon
if not local_intersection_poly.is_empty:
intersection_boundary_linearring.append(local_intersection_poly)
return intersection_boundary_linearring
def fetch_buffer_polygon(trajectories):
# Calculate the avg value along x and y-axis to calculate the avg length of the trajs
avg_traj = np.mean(trajectories, axis=0)
avg_x = np.mean(avg_traj[:, 0])
avg_y = np.mean(avg_traj[:, 1])
updated_center = (avg_x, avg_y)
# Radius to create the buffer
radius = 100.0
# Create the buffer polygon
buffer_polygon = create_buffer_around_coordinate(updated_center, radius)
return buffer_polygon
Putting everything together
The pruning_trajectories function is responsible for refining a set of trajectories based on the drivable areas provided. It takes two inputs: local_das, which represents the drivable area polygons in city coordinates, and rotated_trajectories, which is a list of trajectories in city coordinates that need to be pruned.
Within the function, polygons_restOfMap is created by converting the smaller polygons inside the larger map into Polygon objects, while polygons_wholeOfMap is created by converting the first polygon, which represents the entire map, into a LinearRing object. This distinction is necessary because the larger map encompasses all the smaller polygons, and therefore, requires a different logic for checking trajectory compliance.
To determine if a trajectory has to be removed, two conditions must be met. First, the trajectory must intersect with at least one of the polygons in polygons_restOfMap. Second, the trajectory must be present inside the larger map defined by polygons_wholeOfMap. These checks are performed using the if statement in the function.
However, directly using the complete polygons and checking against all their edges for intersection is computationally inefficient and does not scale well. To address this issue and improve the algorithm’s efficiency, both polygons_wholeOfMap and polygons_restOfMap are reduced to reduced_polygons_wholeOfMap and reduced_polygons_restOfMap, respectively. This reduction process involves calculating the intersection polygons between the original polygons and a buffer polygon derived from the rotated trajectories using the calculate_intersection_polygons and calculate_intersection_polygons_main_map functions.
By reducing the polygons to their relevant intersections with the trajectory buffer, the computation complexity is significantly reduced, and the algorithm becomes more efficient in terms of scaling. The pruning_trajectories function then iterates over each trajectory in rotated_trajectoriesand checks if it intersects with any of the reduced polygons using the check_intersection and check_linestring_intersects functions. Trajectories that satisfy both conditions are considered valid and added to the valid_trajectories list, which is finally returned by the function.
def pruning_trajectories(local_das, rotated_trajectories) -> List[ndarray]:
"""
Function to prune the trajectories based on the drivable area polygon which we retrieve from the map
Param:
local_das: local drivable area polygon in city coordinates. First index is always the whole map represented as an over-lapping polygon so need to be handled with a different logic.
rotated trajectories: list of rotated trajectories in the city coordinates
Returns:
List of pruned trajectories in city coordinates which can further be converted to curvilinear coordinates using rotation matrix.
"""
polygons_restOfMap = [Polygon(polygon) for polygon in local_das[1:]]
polygons_wholeOfMap = [LinearRing(polygon) for polygon in local_das[:1]]
reduced_polygons_restOfMap = calculate_intersection_polygons(polygons_restOfMap, fetch_buffer_polygon(rotated_trajectories))
reduced_polygons_wholeOfMap = calculate_intersection_polygons_main_map(polygons_wholeOfMap, fetch_buffer_polygon(rotated_trajectories))
print(f"Shape of the rotated Trajectories {rotated_trajectories.shape}")
valid_trajectories = []
for i in rotated_trajectories:
if check_intersection(LineString(i), reduced_polygons_restOfMap) and check_linestring_intersects(LineString(i), reduced_polygons_wholeOfMap):
valid_trajectories.append(i)
return valid_trajectories
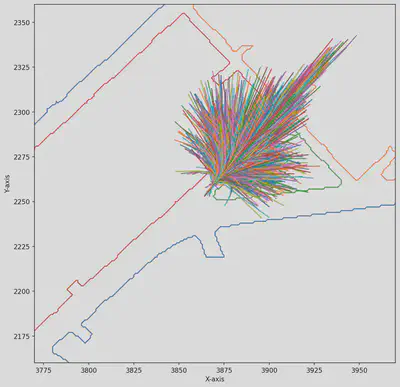
The below for loop is self-explanatory and if we run this whole thing together, we get a refined set which when plotted looks like the following image.
if __name__="__main__":
for i in range(1,10):
# lets create a fig and axes canvas using matplotlib
fig = plt.figure(1, figsize=(10, 10), dpi=150)
ax = fig.add_subplot(111)
# Get the local drivable areas and corresponding rotated trajectories
local_das, trajectories = just_load_das_traj(i)
# local_das[x,y,z] should be made local_das[x,y]
cleaned_local_das = remove_last_dim_from_nested_arrays(local_das)
# Convert the HD map edges from the dataset into polygons using the shapely lib.
refined_set = np.array(pruning_trajectories(local_das, trajectories))
plot_this(clearned_local_das, refined_set, ax)